In this post, I am introducing a solution that uses my interval on a countably
infinite discrete set called IntervalCID CLR user defined type. For more in-depth knowledge about intervals, interval operators, and interval forms, please refer to the Inside Microsoft® SQL Server® 2008: T-SQL Programming book by Itzik Ben-Gan , Dejan Sarka, Roger Wolter, Greg Low , Ed Katibah, and Isaac Kunen, Microsoft Press, 2009 (http://www.amazon.com/gp/product/0735626022/ref=s9_simh_gw_p14_d0_i1?pf_rd_m=ATVPDKIKX0DER&pf_rd_s=center-2&pf_rd_r=1AEWTQ7GTY1XS1R68R2M&pf_rd_t=101&pf_rd_p=1389517282&pf_rd_i=507846). I explain a lot of details in chapter 12, Temporal Support in the Relational Model.
I am showing the C# definition of the IntervalCID type here, as a block comment inside T-SQL code. As I mentioned, please refer to the book for the details of this type, Allen’s operators, and more. If you want to test this code, just create a C# CLR UDT project, copy the code, and compile it.
— IntervalCID C# code
/*
using System;
using System.Data;
using System.Data.SqlClient;
using System.Data.SqlTypes;
using Microsoft.SqlServer.Server;
using System.Text.RegularExpressions;
using System.Globalization;
[Serializable]
[Microsoft.SqlServer.Server.SqlUserDefinedType(
Format.Native,
IsByteOrdered = true,
ValidationMethodName = “ValidateIntervalCID”)]
public struct IntervalCID : INullable
{
//Regular expression used to parse values of the form (intBegin,intEnd)
private static readonly Regex _parser
= new Regex
(@”A(s*(?
RegexOptions.Compiled | RegexOptions.ExplicitCapture);
// Begin, end of interval
private Int32 _begin;
private Int32 _end;
// Internal member to show whether the value is null
private bool _isnull;
// Null value returned equal for all instances
private const string NULL = “<
private static readonly IntervalCID NULL_INSTANCE
= new IntervalCID(true);
// Constructor for a known value
public IntervalCID(Int32 begin, Int32 end)
{
this._begin = begin;
this._end = end;
this._isnull = false;
}
// Constructor for an unknown value
private IntervalCID(bool isnull)
{
this._isnull = isnull;
this._begin = this._end = 0;
}
// Default string representation
public override string ToString()
{
return this._isnull ? NULL : (“(“
+ this._begin.ToString(CultureInfo.InvariantCulture) + “:”
+ this._end.ToString(CultureInfo.InvariantCulture)
+ “)”);
}
// Null handling
public bool IsNull
{
get
{
return this._isnull;
}
}
public static IntervalCID Null
{
get
{
return NULL_INSTANCE;
}
}
// Parsing input using regular expression
public static IntervalCID Parse(SqlString sqlString)
{
string value = sqlString.ToString();
if (sqlString.IsNull || value == NULL)
return new IntervalCID(true);
// Check whether the input value matches the regex pattern
Match m = _parser.Match(value);
// If the input’s format is incorrect, throw an exception
if (!m.Success)
throw new ArgumentException(
“Invalid format for complex number. “
+ “Format is (intBegin:intEnd).”);
// If everything is OK, parse the value;
// we will get two Int32 type values
IntervalCID it = new IntervalCID(Int32.Parse(m.Groups[1].Value,
CultureInfo.InvariantCulture), Int32.Parse(m.Groups[2].Value,
CultureInfo.InvariantCulture));
if (!it.ValidateIntervalCID())
throw new ArgumentException(“Invalid begin and end values.”);
return it;
}
// Begin and end separately
public Int32 BeginInt
{
[SqlMethod(IsDeterministic = true, IsPrecise = true)]
get
{
return this._begin;
}
set
{
Int32 temp = _begin;
_begin = value;
if (!ValidateIntervalCID())
{
_begin = temp;
throw new ArgumentException(“Invalid begin value.”);
}
}
}
public Int32 EndInt
{
[SqlMethod(IsDeterministic = true, IsPrecise = true)]
get
{
return this._end;
}
set
{
Int32 temp = _end;
_end = value;
if (!ValidateIntervalCID())
{
_end = temp;
throw new ArgumentException(“Invalid end value.”);
}
}
}
// Validation method
private bool ValidateIntervalCID()
{
if (_end >= _begin)
{
return true;
}
else
{
return false;
}
}
// Allen’s operators
public bool Equals(IntervalCID target)
{
return ((this._begin == target._begin) &
(this._end == target._end));
}
public bool Before(IntervalCID target)
{
return (this._end < target._begin);
}
public bool After(IntervalCID target)
{
return (this._begin > target._end);
}
public bool Includes(IntervalCID target)
{
return ((this._begin <= target._begin) &
(this._end >= target._end));
}
public bool ProperlyIncludes(IntervalCID target)
{
return ((this._begin < target._begin) &
(this._end > target._end));
}
public bool Meets(IntervalCID target)
{
return ((this._end + 1 == target._begin) |
(this._begin == target._end + 1));
}
public bool Overlaps(IntervalCID target)
{
return ((this._begin <= target._end) &
(target._begin <= this._end));
}
public bool Merges(IntervalCID target)
{
return (this.Meets(target) |
this.Overlaps(target));
}
public bool Begins(IntervalCID target)
{
return ((this._begin == target._begin) &
(this._end <= target._end));
}
public bool Ends(IntervalCID target)
{
return ((this._begin >= target._begin) &
(this._end == target._end));
}
public IntervalCID Union(IntervalCID target)
{
if (this.Merges(target))
return new IntervalCID(
System.Math.Min(this.BeginInt, target.BeginInt),
System.Math.Max(this.EndInt, target.EndInt));
else
return new IntervalCID(true);
}
public IntervalCID Intersect(IntervalCID target)
{
if (this.Merges(target))
return new IntervalCID(
System.Math.Max(this.BeginInt, target.BeginInt),
System.Math.Min(this.EndInt, target.EndInt));
else
return new IntervalCID(true);
}
public IntervalCID Minus(IntervalCID target)
{
if (this.Merges(target) &
(this.BeginInt < target.BeginInt) &
(this.EndInt <= target.EndInt))
return new IntervalCID(
this.BeginInt,
System.Math.Min(target.BeginInt – 1, this.EndInt));
else
if (this.Merges(target) &
(this.BeginInt >= target.BeginInt) &
(this.EndInt > target.EndInt))
return new IntervalCID(
System.Math.Max(target.EndInt + 1, this.BeginInt),
this.EndInt);
else
return new IntervalCID(true);
}
}
*/
As mentioned, I am not going into a detailed explanation of the data type. Let me just point out that it uses native serialization, which is byte ordered (see the attributes of the structure), and that the two private variables which denote the begin and the end of the interval appear in the order begin, end. This means that the order of the intervals when serialized is (begin, end), like the following list example shows:
(1, 3)
(1, 5)
(2, 2)
(3, 4)
(3, 7)
(4, 5)
To show this graphically, the following picture denotes the order of the intervals.
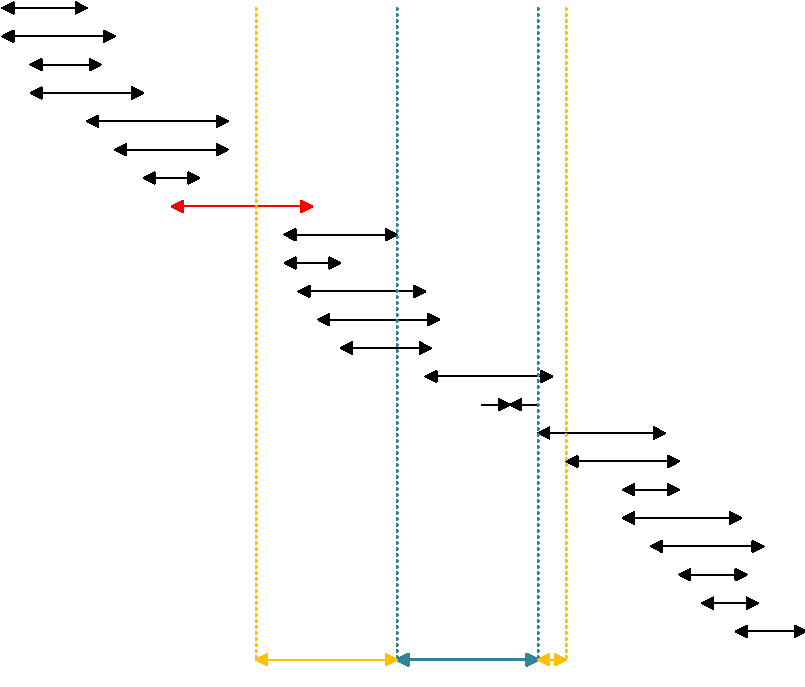
Black color denotes the intervals in the table. The blue colored interval is the one I am checking for the overlaps. The intervals are sorted by the lower boundary, representing SQL Server’s usage of the idx_lower index. Eliminating intervals from the right side of the given (blue) interval is simple: just eliminate all intervals where the beginning is at least one unit bigger (more to the right) of the end of the given interval. You can see this boundary in the figure denoted with yellow line. However, eliminating from the left is more complex. In order to use the same index, the index which I will create on the column of my IntervalCID data type for eliminating from the left, I need to use the beginning of the intervals in the table in the WHERE clause of the query. I have to go to the left side away from the beginning of the given (blue) interval at least for the length of the longest interval in the table, which is marked with red color in the figure. Of course, this picture is taken from the first blog post in this series, the Interval Queries in SQL Server Part 1 post. I could just provide the link; however, I spent quite a few time for drawing this picture in Visio, and therefore I want to publish it more than onceJ Don’t you agree that it is very nice?
In order to use a CLR data type, you need to enable CLR on your SQL Server instance.
USE
master;
EXEC
sp_configure
‘clr enabled’, 1;
RECONFIGURE;
GO
USE
IntervalsDB;
GO
The next step is to deploy the assembly and create the data type.
— Deploy assembly
— Replace the path with your path to the .dll file
CREATE
ASSEMBLY
IntervalCID
FROM
‘C:TempIntervalCID.dll’
WITH
PERMISSION_SET
=
SAFE;
GO
— Type
CREATE
TYPE
dbo.IntervalCID
EXTERNAL NAME
IntervalCID.IntervalCID;
GO
Now I can create and populate a table that uses the IntervalCID data type to store the intervals. Note that I am also creating an index on my IntervalCID column called during.
CREATE
TABLE
dbo.IntervalsCID
(
id
INT
NOT
NULL,
during
IntervalCID
NOT
NULL
);
INSERT
INTO
dbo.IntervalsCID
WITH(TABLOCK)
(id, during)
SELECT
id,
N'(‘
+
CAST(lower
AS
NVARCHAR(10))
+‘:’ +
CAST(upper
AS
NVARCHAR(10))
+
‘)’
FROM
dbo.Stage;
ALTER
TABLE
dbo.IntervalsCID
ADD
CONSTRAINT
PK_IntervalsCID
PRIMARY
KEY(id);
CREATE
INDEX
idx_IntervalCID
ON
dbo.IntervalsCID(during);
GO
Executing this part of code took approximately 80 second on my notebook. Therefore, the performance is pretty good, nearly the same as with the fastest solution I tested so far.
For querying, the query is quite similar to the query introduced in the part 1 of this series. I find the maximal length of the intervals in advance and then store it in a variable (OK, this time I already know the maximal length is 20, so I store this as a constant and don’t query for it anymore). The query that checks for the overlaps in the middle of the data uses just slightly different WHERE clause than the query in the part 1; instead of just using the @l and @u variables that define the given, the searched interval, I need to create three variables of IntervalCID data type:
- An interval whose sort value is low enough to filter out the intervals before the given one
- An interval whose sort value is high enough to filter out the intervals after the given one
- An interval to filter exactly the intervals needed, the ones that really overlap with the given one
Here is the code for the query the middle of the data:
— query
SET
STATISTICS
IO
ON;
SET
STATISTICS
TIME
ON;
GO
— middle of data
DECLARE
@l
AS
INT
= 5000000,
@u
AS
INT
= 5000020;
DECLARE
@max
AS
INT
= 20;
— max length in the data is 20
DECLARE
@b
AS
IntervalCID, @e
AS
IntervalCID, @i
AS
IntervalCID;
— An interval whose sort value is low enough to filter out
— the intervals before the given one
SET @b
=
N'(‘
+
CAST((@l – 1 –
@max)
AS
NVARCHAR(10))
+
‘:’
+
CAST((@l–1)
AS
NVARCHAR(10))
+
‘)’;
— An interval whose sort value is high enough to filter out
— the intervals after the given one
SET
@e
= N'(‘
+
CAST((@u+1)
AS
NVARCHAR(10))
+
‘:’
+
CAST((@u +1)
AS
NVARCHAR(10))
+
‘)’;
— An interval to filter exactly the intervals needed,
— the ones that really overlap with the given one
SET
@i
= N'(‘
+
CAST(@l
AS
NVARCHAR(10))
+‘:’
+
CAST(@u
AS
NVARCHAR(10))
+
‘)’;
SELECT
id
FROM
dbo.IntervalsCID
AS
I
WHERE
during < @e AND
during
>
@b
AND
@i.Overlaps(I.during)
= 1
OPTION (RECOMPILE);
GO
— logical reads: 4, CPU time: 0 ms
As you can see, the code is extremely efficient. The query performs perfectly. However, the query has the same problem as the query introduced in part 1. If there would be only one long interval in the table, the code would become much less efficient, because SQL Server would not be able to eliminate a lot of rows from the left side of the given interval.
Nevertheless, using the IntervalCID data type is my preferred solution so far. First of all, because the knowledge built in the data type, for example Allen’s operators, the T-SQL code becomes simple and less prone to errors. You can quickly change the query to check for the included intervals, intervals that begin other intervals, and similar. Just select the operator you need. In addition, the during column is now a scalar column, which eliminates problems with normalization. Note that in Itzik’s demo data, the id column is unique. However, imagine a real world case, for example a table of the products supplied. This table would have in the classical solution at least these four columns: supplierid, productid, lower, upper. Because the same supplier can supply the same product in different time periods, the combination supplierid, productid cannot be a key for this table. There are two candidate keys: supplierid, productid, lower and supplierid, productid, upper. Two composite candidate keys with overlapping columns violate the Boyce-Codd normal form. This problem disappears when the only candidate key is supplierid, productid, during.
Besides this kind of optimization of the interval queries I just introduced in this post, it is possible to use all other optimizations I know and I have introduced in the previous posts in this series, including the RI tree model introduced in Itzik’s article, and except the geometry data type solution by Davide Mauri (of course, a single column cannot be of two data types). You can create persisted calculated columns from the IntervalCID data type properties to get a single lower and upper boundary values, to calculate the fork node for the RI tree model, or to create an indexed view or an additional table in the unpacked form.
Again, I have to rant about Microsoft. It is not possible to use CLR UDT properties directly in indexes, constraints like foreign keys, and more. That’s why I need to add persisted computed columns and thus denormalize my table. This lowers the usability of the CLR UDTs.
Here is the code that creates the dbo.IntervalsCID table with all computed persisted columns you might need:
CREATE
TABLE
dbo.IntervalsCID
(
id
INT
NOT
NULL,
during
IntervalCID
NOT
NULL,
lower
AS
during.BeginInt
PERSISTED,
upper
AS
during.EndInt
PERSISTED,
ilen
AS
during.EndInt – during.BeginInt
PERSISTED,
node
AS
during.EndInt – during.EndInt %
POWER(2, FLOOR(LOG((during.BeginInt – 1)
^ during.EndInt, 2)))
PERSISTED
);
Now you can just pick up the optimized interval queries solution that suits you and your data the best.


