| Actual | |||
| Gender |
Married |
Single |
Total |
| F |
4745 |
4388 |
9133 |
| M |
5266 |
4085 |
9351 |
| Total |
10011 |
8473 |
18484 |
| Expected | |||
| Gender |
Married |
Single |
Total |
| F |
4946 |
4187 |
9133 |
| M |
5065 |
4286 |
9351 |
| Total |
10011 |
8473 |
18484 |
If the columns are not contingent on the rows, then the rows and column frequencies are independent. The test of whether the columns are contingent on the rows is called the chi-square test of independence. The null hypothesis is that there is no relationship between row and column frequencies. Therefore, there should be no difference between the observed and expected frequencies. Contingency tables are the base for the chi-square test. However, even without the test, you might notice some relationship between two discrete variables just by seeing the contingency table.
Contingency tables are very simple to interpret, and therefore they are a very popular tool in statistics and data mining. Wouldn’t it be nice to have a possibility to create such a nice contingency table checking the association between NumberCarsOwned and BikeBuyer columns from the dbo.vTargetMail like the following screenshot shows with SQL Server tools?
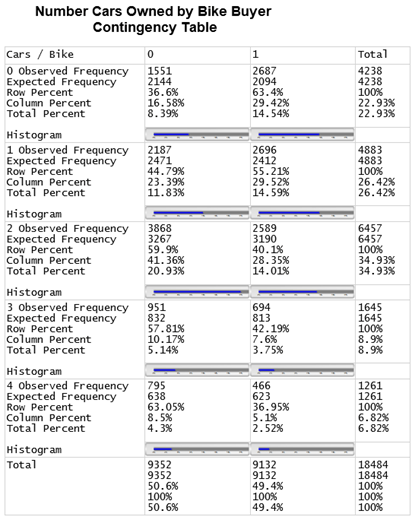
Of course, I would not write this blog if I would not have a solution. The screenshot above is actually a screenshot of a SQL Server 2012 Reporting Services (SSRS) report. The whole story starts with the following query.
WITH
ObservedCombination_CTE
AS
(
SELECT
NumberCarsOwned
AS
OnRows,
BikeBuyer
AS
OnCols,
COUNT(*)
AS
ObservedCombination
FROM
dbo.vTargetMail
GROUP
BY
NumberCarsOwned, BikeBuyer
)
SELECT
OnRows, OnCols, ObservedCombination
,SUM(ObservedCombination)
OVER (PARTITION
BY
OnRows)
AS ObservedOnRows
,SUM(ObservedCombination)
OVER (PARTITION
BY
OnCols)
AS ObservedOnCols
,SUM(ObservedCombination)
OVER () AS ObservedTotal
,CAST(ROUND(SUM(1.0 *
ObservedCombination)
OVER (PARTITION
BY
OnRows)
*
SUM(1.0 *
ObservedCombination)
OVER (PARTITION
BY
OnCols)
/
SUM(1.0 *
ObservedCombination)
OVER (), 0) AS
INT) AS ExpectedCombination
,CAST(ROUND(100.0 *
ObservedCombination
/
SUM(ObservedCombination)
OVER (), 0) AS
INT)
AS
PctTotal
,REPLICATE(‘*’,
CAST(ROUND(100.0 *
ObservedCombination
/
SUM(ObservedCombination)
OVER (), 0) AS
INT))
AS
Histogram
FROM
ObservedCombination_CTE
ORDER
BY
OnRows, OnCols
Note that the query uses the new window functions in SQL Server 2012. The result of this query is not pivoted yet, however it contains all of the data needed.
| OnRows |
OnCols |
Observed Combination |
Observed On Rows |
Observed On Cols |
Observed Total |
Expected Combination |
PctTotal |
Histogram |
| 0 |
0 |
1551 |
4238 |
9352 |
18484 |
2144 |
8 |
******** |
| 0 |
1 |
2687 |
4238 |
9132 |
18484 |
2094 |
15 |
*************** |
| 1 |
0 |
2187 |
4883 |
9352 |
18484 |
2471 |
12 |
************ |
| 1 |
1 |
2696 |
4883 |
9132 |
18484 |
2412 |
15 |
*************** |
| 2 |
0 |
3868 |
6457 |
9352 |
18484 |
3267 |
21 |
********************* |
| 2 |
1 |
2589 |
6457 |
9132 |
18484 |
3190 |
14 |
************** |
| 3 |
0 |
951 |
1645 |
9352 |
18484 |
832 |
5 |
***** |
| 3 |
1 |
694 |
1645 |
9132 |
18484 |
813 |
4 |
**** |
| 4 |
0 |
795 |
1261 |
9352 |
18484 |
638 |
4 |
**** |
| 4 |
1 |
466 |
1261 |
9132 |
18484 |
623 |
3 |
*** |
Next part is to create the report. Use the Matrix (OK, Tablix with row and column groups) control. The trick is what to put in the cells of the matrix. The following screenshot shows the expression used for the most detailed cell of the matrix.
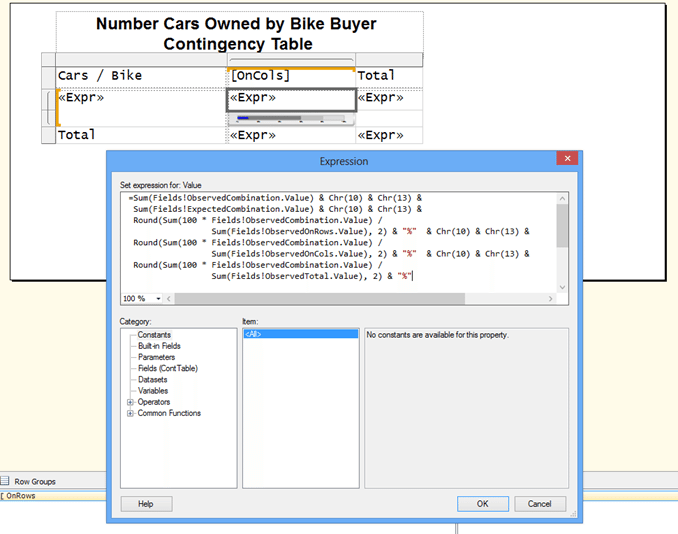
Similar expression are used for other cells with data. The expression for the column total, i.e. for the cell that is the intersection of the [OnCols] column and Total row, is
=Sum(Fields!ObservedCombination.Value) & Chr(10) & Chr(13) &
Sum(Fields!ExpectedCombination.Value) & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedOnRows.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedCombination.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedOnRows.Value), 2) & “%” & Chr(10) & Chr(13)
The expression for the row totals is
=Sum(Fields!ObservedCombination.Value) & Chr(10) & Chr(13) &
Sum(Fields!ExpectedCombination.Value) & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedCombination.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedOnCols.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedOnCols.Value), 2) & “%” & Chr(10) & Chr(13)
The expression for the grand total cell is
=Sum(Fields!ObservedCombination.Value) & Chr(10) & Chr(13) &
Sum(Fields!ExpectedCombination.Value) & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedCombination.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedCombination.Value), 2) & “%” & Chr(10) & Chr(13) &
Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedCombination.Value), 2) & “%” & Chr(10) & Chr(13)
The expression for the row header is
=Fields!OnRows.Value & ” Observed Frequency” & Chr(10) & Chr(13) &
” Expected Frequency” & Chr(10) & Chr(13) &
” Row Percent” & Chr(10) & Chr(13) &
” Column Percent” & Chr(10) & Chr(13) &
” Total Percent” & Chr(10) & Chr(13) &
Chr(10) & Chr(13) &
” Histogram”
The expression for the value of the linear pointer of the gauge is
= Round(Sum(100 * Fields!ObservedCombination.Value) /
Sum(Fields!ObservedTotal.Value), 2)
And the expression for the max value for the gauge scale is
=Max(Fields!PctTotal.Value, “ContTable”)
This all together looks like a lot of work. However, it is not that bad. The source query is not too complicated, and you can easily change the columns and the table used for the analysis, as their names appear once in the common table expression only. The report does not refer to the source names anywhere, so it is simple to copy it and use for a new report with a contingency table for two different columns. You just need to change the report header and the top left cell text of the matrix, which shows the columns used for the report.


